Page 1 of 1
Summing series
Posted: Tue May 03, 2011 7:01 pm
by Gavin Chipper
This isn't really a puzzle that I'm setting, but something I want to know the answer to. I'm not sure if this is something that's actually quite trivial and I'm just being thick. Is there a simple formula for:
1 + 1/2 + 1/3 + 1/4 +...+ 1/n
also
1 + 1/3 + 1/5 + 1/7 + ... + 1/(2n-1)?
Thanks in advance.
Re: Summing series
Posted: Tue May 03, 2011 7:59 pm
by Gavin Chipper
http://mathworld.wolfram.com/HarmonicNumber.html
A harmonic number can be expressed analytically as
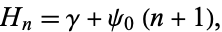
where
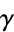
is the Euler-Mascheroni constant and
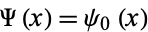
is the digamma function.
Piece of piss.

Edit:
Euler–Mascheroni constant
http://en.wikipedia.org/wiki/Euler%E2%8 ... i_constant
Its numerical value to 50 decimal places is
0.57721 56649 01532 86060 65120 90082 40243 10421 59335 93992
That bit's OK. It's the digamma function that looks an arse. And this is just for 1 + 1/2 etc. I wouldn't know where to start with the other one.
Re: Summing series
Posted: Tue May 03, 2011 8:10 pm
by Charlie Reams
Gavin Chipper wrote:
That bit's OK. It's the digamma function that looks an arse. And this is just for 1 + 1/2 etc. I wouldn't know where to start with the other one.
gamma + ln(n) is a pretty good approximation (in the limit).
For the other one you can use the fact that
1 + 1/3 + 1/5 + ... + 1/n
= (1 + 1/2 + ... + 1/n) - (1/2 + 1/4 + 1/6 + ... + 1/(n-1))
= H_n - (1/2) (1 + 1/2 + 1/3 + ... + 1/((n-1)/2) )
= H_n - (1/2) * H_{(n-1)/2}
(I just did that so I might've screwed up one of the limits but you get the idea.)
Re: Summing series
Posted: Tue May 03, 2011 9:09 pm
by Peter Mabey
That reminds me of another problem I've been thinking about recently (stimulated by one of
Professor Stewart's Hoard of Mathematical Treasures.
How do you find an efficient way of expressing integers n>1 as Egyptian Fractions?
The greedy algorithm becomes increasingly inefficient as it pulls in more and more primes with increasing n, whilst better solutions are given by the known multiperfect numbers, which are clearly not the best, though the factors of abundant numbers look to be the most promising line of attack.
The best for n=2 I've got so far is {2,3,4,5,6,8,9,10,12,15,18} - with the obvious notation, and maximizing the smallest fraction. I haven't found one with fewer terms, even by going down to smaller fractions

Re: Summing series
Posted: Tue May 03, 2011 9:14 pm
by Charlie Reams
Peter Mabey wrote:That reminds me of another problem I've been thinking about recently (stimulated by one of
Professor Stewart's Hoard of Mathematical Treasures.
How do you find an efficient way of expressing integers n>1 as Egyptian Fractions?
The greedy algorithm becomes increasingly inefficient as it pulls in more and more primes with increasing n, whilst better solutions are given by the known multiperfect numbers, which are clearly not the best, though the factors of abundant numbers look to be the most promising line of attack.
The best for n=2 I've got so far is {2,3,4,5,6,8,9,10,12,15,18} - with the obvious notation, and maximizing the smallest fraction. I haven't found one with fewer terms, even by going down to smaller fractions

Given that the harmonic series diverges incredibly slowly, you shouldn't expect to be able to find compact solutions. Not very helpful, I know. Is it even possible to solve for every n? (Edit: Yes.)
Re: Summing series
Posted: Tue May 03, 2011 9:39 pm
by Charlie Reams
Peter Mabey wrote:That reminds me of another problem I've been thinking about recently (stimulated by one of Professor Stewart's Hoard of Mathematical Treasures.
How do you find an efficient way of expressing integers n>1 as Egyptian Fractions?
I know this isn't exactly your problem, but I found this on
Mathworld: "No algorithm is known for producing unit fraction representations having either a minimum number of terms or smallest possible denominator" which suggests that your algorithm isn't known either.
Re: Summing series
Posted: Tue May 03, 2011 11:32 pm
by Gavin Chipper
By the way, the reason I asked the original question was that I've been comparing the
Sainte-Laguë and D'Hondt systems of allocating seats in elections. As far as I understand, they both give proportional representation when a party's proportion of the vote matches exactly with a whole number of seats. I was hoping to get the formula for fractional seats and "break" one of the systems. There's probably a much easier way though.
Re: Summing series
Posted: Tue May 03, 2011 11:35 pm
by Charlie Reams
Gavin Chipper wrote:By the way, the reason I asked the original question was that I've been comparing the
Sainte-Laguë and D'Hondt systems of allocating seats in elections. As far as I understand, they both give proportional representation when a party's proportion of the vote matches exactly with a whole number of seats. I was hoping to get the formula for fractional seats and "break" one of the systems. There's probably a much easier way though.
You're welcome.
Re: Summing series
Posted: Tue May 03, 2011 11:37 pm
by Gavin Chipper
Charlie Reams wrote:Gavin Chipper wrote:By the way, the reason I asked the original question was that I've been comparing the
Sainte-Laguë and D'Hondt systems of allocating seats in elections. As far as I understand, they both give proportional representation when a party's proportion of the vote matches exactly with a whole number of seats. I was hoping to get the formula for fractional seats and "break" one of the systems. There's probably a much easier way though.
You're welcome.
Haha - I was going to say thank you a few hours ago but decided to do so next time I posted. Then forgot. Thanks!
Edit - actually
Gavin Chipper wrote:Thanks in advance.

Re: Summing series
Posted: Tue May 03, 2011 11:50 pm
by Charlie Reams
Gavin Chipper wrote:Edit - actually
Gavin Chipper wrote:Thanks in advance.

Haha. Dick. Thanks accepted (both times).
Re: Summing series
Posted: Tue May 03, 2011 11:51 pm
by Michael Wallace
Charlie Reams wrote:Gavin Chipper wrote:Edit - actually
Gavin Chipper wrote:Thanks in advance.

Haha. Dick. Thanks accepted (both times).
Christ, get a room you homos.
Re: Summing series
Posted: Tue May 03, 2011 11:54 pm
by Gavin Chipper
Just found
this.
Edit - D'Hondt broke and Saintë-Lague didn't so there you go.
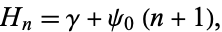
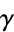 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 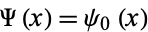 is the digamma function.
is the digamma function.